ES1ere Ch1 La forme de la terre suite
Ajouter à mes favoris
Distance à la surface de la terre
question 1
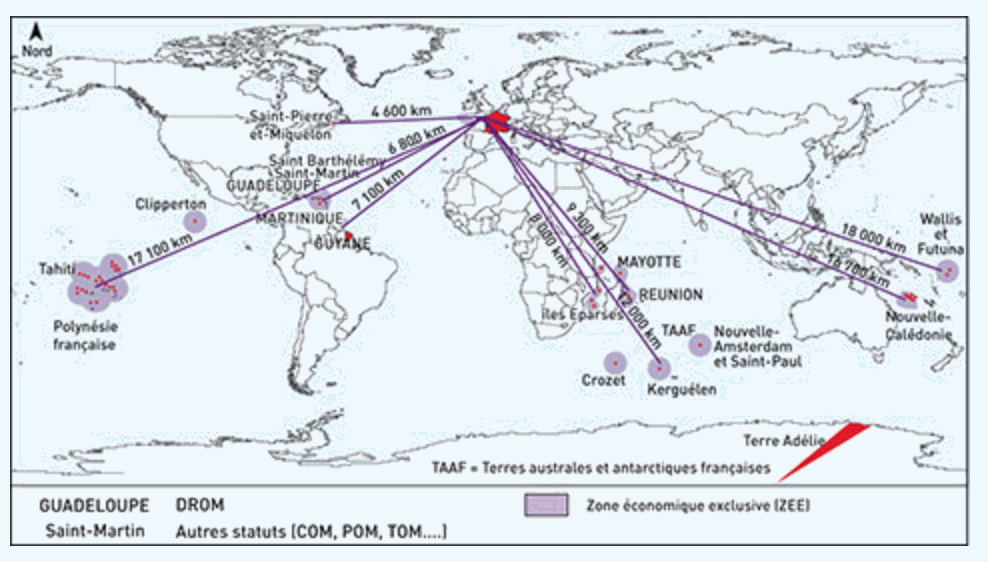
Le planisphère ci-contre montre les distances entre la métropole et plusieurs départements et territoires d'outre-mer.
On s'intéresse au trajet en avion liant, par exemple, Paris à Nouméa (Nouvelle-Calédonie), en supposant un vol direct.
Indiquez les pays survolés lors du trajet Paris-Nouméa, en supposant que le trajet suivi est le segment représenté ci-contre :
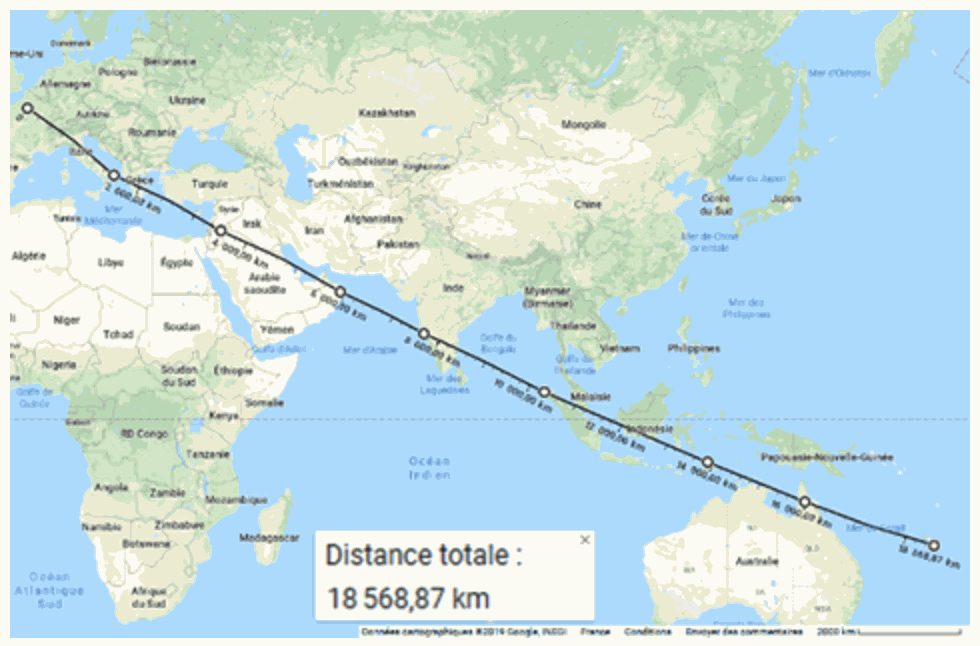
Le planisphère ci-contre montre un trajet direct de Paris à Nouméa, en « ligne droite ». Les pays survolés sont les mêmes que sur le planisphère précédent.
Le tracé et la mesure de distance ont été relevés à l'aide d'un site internet bien connu de localisation et de cartographie.
La distance parcourue, d'après la figure ci-contre, est-elle :
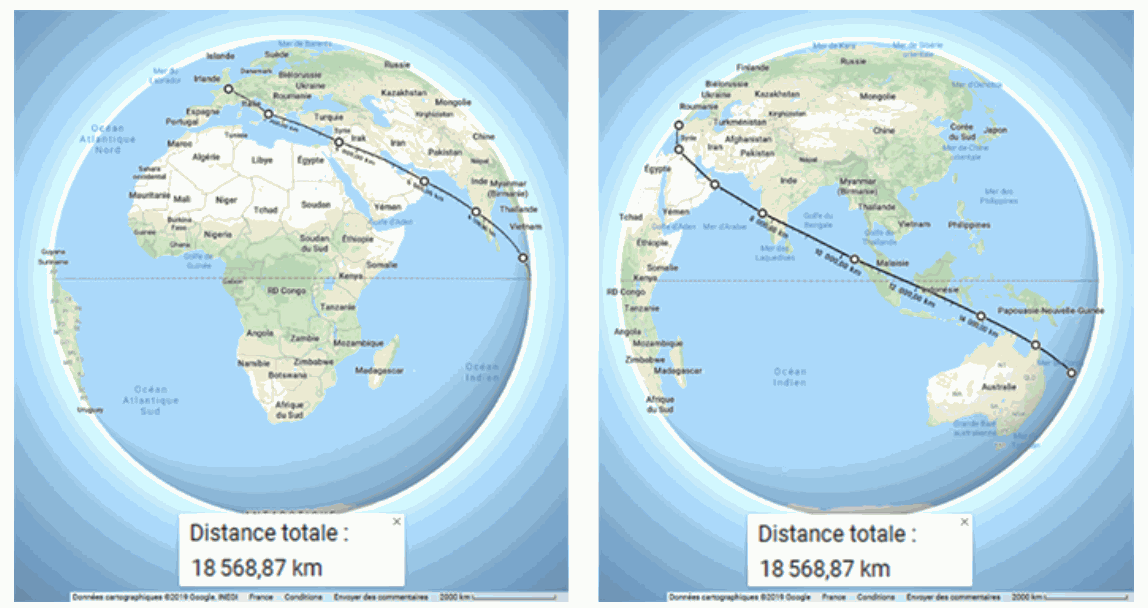
Le trajet suivi sur les pages précédentes semblait être le plus court car il était « en ligne droite » sur le planisphère.
Or, la Terre est ronde, et les figures ci-contre ont montré la forme de ce même trajet à la surface du globe terrestre.
Le trajet suivi est-il :
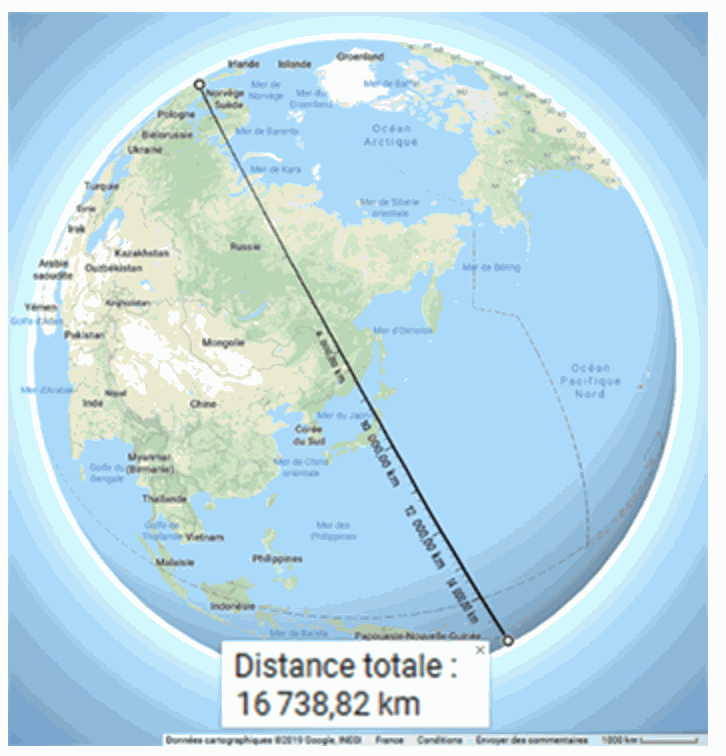
Dans le plan, « le plus court chemin entre deux points est une ligne droite ».
Le chemin le plus direct doit donc avoir l'apparence d'un segment de droite, vu à la surface du globe : la figure ci-contre montre un tel chemin.
La distance parcourue, d'après la figure ci-contre, est-elle :

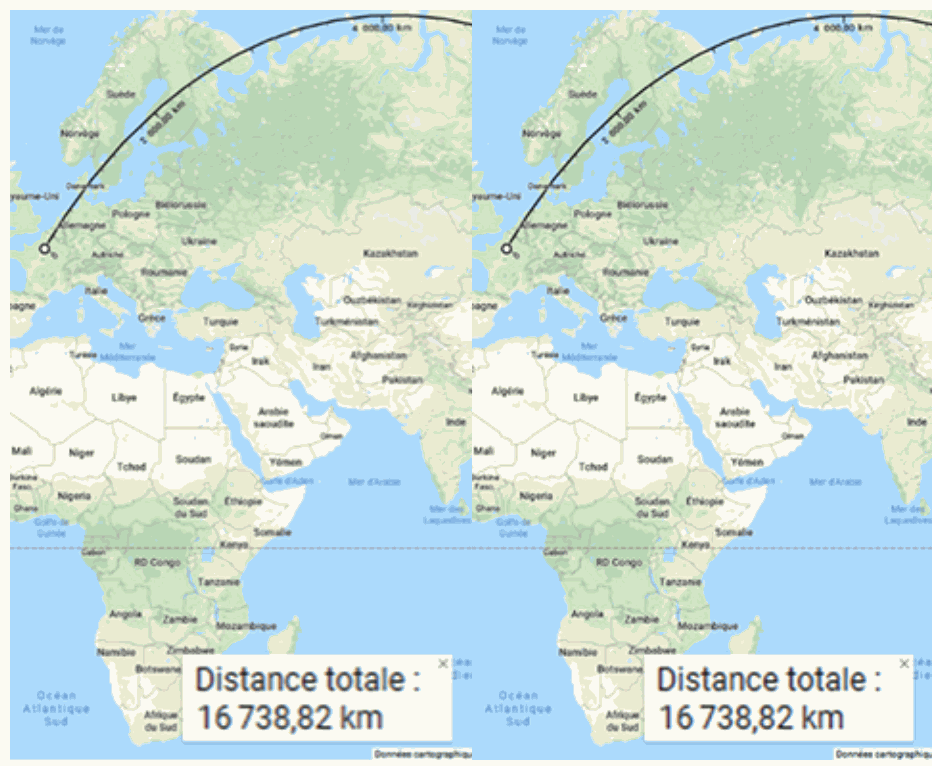
La figure ci-contre montre le trajet précédent, représentée sur un planisphère. On a montré qu'il s'agit bien du chemin le plus court, compte tenu de la forme de la Terre.
On imagine à nouveau un trajet en avion, sans escale, de Paris à Nouméa.
Indiquez les pays survolés lors du trajet Paris-Nouméa, en supposant que le trajet suivi est représenté ci-contre :
Activité 3 : méthode de plan de triangulation
Introduction
- Application de la relation des sinus pour la détermination d'une distance.
Illustration : pictogrammes représentant les mathématiques
s.
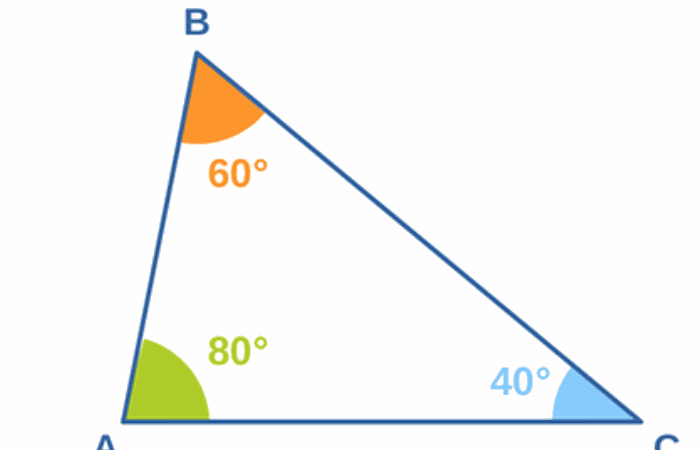
Voici la relation appelée « loi des sinus » dans un triangle ABC :
On la doit aux travaux du mathématicien persan Abu Nasr Mansur (~960 – 1036).
Complétez le texte à trois suivants.
La longueur d'un des côtés est connue : AB = 30 km. En utilisant la loi des sinus, on peut écrire la longueur BC =
Numériquement, BC = .
Que retenir
|
La longueur d'un arc de cercle est égale au produit du rayon du cercle et de l'angle défini cet arc, exprimé en radians :
On peut alors calculer des distances à la surface de la Terre :
avec et les latitudes de A et B, en radians et RT le rayon de la Terre.
avec LA et LC les longitudes de A et C, en radians.
Le plus court chemin entre deux points à la surface de la Terre est l'arc du grand cercle qui les relie.On peut calculer une distance entre 2 points B et C assez proches (au plus quelques dizaines de km) par une méthode de triangulation avion, connaissant la distance d'un de ces points à un troisième point A (par exemple AB), ainsi que l'angle entre les deux visées (angle de sommet A). |
APPRENDRE Activité 1 La figure de la terre Introduction
- Astronomie et géodésie ;
- Évolution de la « figure de la Terre » de l'Antiquité à nos jours ;
- Distinction des arguments philosophiques et des arguments scientifiques.
Illustration : représentation du Système Solaire et carte du ciel.
question 1
Cette partie décrit plusieurs études de géodésie réalisées par des astronomes. Ces disciplines sont voisines mais différentes :
- L'astronomie est l'étude des astres.
- La géodésie est l'étude de la forme de la Terre.
Indiquez dans la liste suivante les problématiques astronomie ou géodésie auxquelles répondent chacune de ces sciences :
|
La "simple" curiosité scientifique est une raison suffisante de poursuivre l'une ou l'autre de ces disciplines, afin de mieux comprendre le monde qui nous entoure. Cependant, ces deux sciences ont (ou ont eu) des utilités pratiques précises.
Indiquez quelle science astronomie ou géodésie, selon vous, permet chacun des usages ci-dessous :
|
Un peu d'histoire
On appelle « Figure de la Terre » la représentation que nous faisons de la forme de notre planète et de ses dimensions géométriques. Cette représentation a évolué avec le temps, avec des influences propres à chaque région du monde et à chaque culture. En Europe occidentale par exemple :
- Les philosophes Grecs, dès -600, notamment Thalès de Milet et Pythagore, établissant entre autres la sphéricité de la Terre.
- Aristote (vers -350) et Ptolémée (vers 150) présentent les arguments suivants pour justifier la sphéricité de la Terre : la forme de l'ombre projetée par la Terre sur la Lune durant les éclipses de Lune ; la variation, avec le lieu d'observation du champ d'étoiles observables ; le fait que les navires s'éloignant de la côte « disparaissent progressivement », masqués par la courbure de l'horizon.
- Ces travaux sont transmis et augmentés par les mathématiciens astronomes arabes, avec notamment l'invention de la trigonométrie (au Xe s. Al-Badtani a introduit la notion de sinus et des méthodes de calcul pour les triangles sphériques), la construction de catalogues détaillés des étoiles, des relevés des éclipses et des conjonctions (notamment Al-Sufi au Xe s.), le développement de l'astrolabe, un instrument d'observation et de calcul astronomique.
Plus récemment
- En Europe occidentale une théorie de la Terre plate basée sur les mythes antiques et chrétiens est imposée jusqu'au XIIIe s., où les travaux des philosophes, mathématiciens, et astronomes sont « redécouverts » et enseignés à l'Université.
- Des mathématiciens, astronomes, et physiciens comme Giordano Bruno, Copernic, Galilée, éclairé que non seulement la Terre est ronde mais qu'elle n'est pas immobile au centre de l'Univers, se basant pour cela sur des observations astronomiques.
- Delambre et Méchain, Picard, Cassini, fournissent plusieurs mesures du méridien terrestre, et donc du rayon de la Terre (sphérique).
- Des mesures ultérieures ont démontré que la Terre n'est pas parfaitement sphérique mais légèrement aplatie aux pôles.
-
Activité 2 : Mesure du méridien terrestre par Eratosthène
Introduction
- Contexte et motivation ;
- Méthode de mesure : théorie et mise en œuvre ;
Illustration : globe terrestre et méridien d'Alexandrie.
Contexte
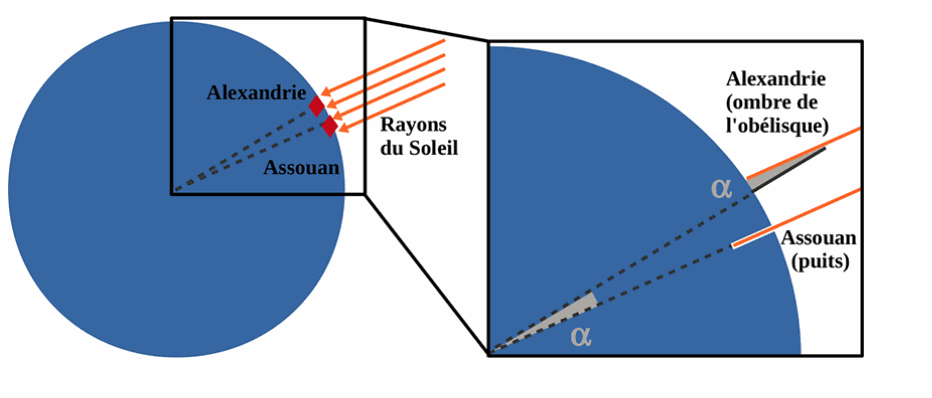
Ératosthène de Cyrène était un astronome, géographe, philosophe et mathématicien grec du IIIᵉ siècle av. J.-C. Il a été directeur de la grande bibliothèque d'Alexandrie. Vers -300, il réalise une mesure du rayon de la Terre (alors supposée de forme sphérique). Il avait remarqué que le 22 juin (jour du solstice d'été), le Soleil était au zénith à Syène (près de l'actuelle Assouan), mais pas à Alexandrie.
Voici ses hypothèses : les rayons du Soleil arrivent parallèlement entre eux du fait de la grande distance de la Terre au Soleil, la Terre est sphérique, les deux villes sont sur le même méridien.
question 1
Complétez le texte à trous suivant à l'aide des indications fournies :
Au même moment, à Alexandrie, Eratosthène mesure un angle de 7° entre les rayons
du Soleil et la verticale ce qui correspond à radians.
question 2
Complétez le texte à trous suivant à l'aide des indications fournies :
Eratosthène a pu déduire la valeur du rayon terrestre RT à partir de l'angle α et de la distance d'entre les 2 villes,
Quelle expression mathématique at 'il utilisée ?............. .......................
D'où une estimation du rayon de la Terre de
question 3
Complétez le texte à trous suivant à l'aide des indications fournies :
Finalement quelle est la longueur du méridien terrestre mesurée par Eratosthène ? .........................km env
Activité 2 : Mesure du méridien terrestre par Delambre et Méchain Introduction
- Contexte et motivation ;
- Méthode de mesure : théorie et mise en œuvre ;
- Résultat de la mesure : précision et discussion.
Illustration : représentation du Système Solaire et carte du ciel.
Contexte
Dans l'Ancien Régime en France, les unités de mesure de longueur telles que le lieu, la toise, etc. étaient utilisées mais leur définition pouvait varier d'une région à l'autre.
Lors de la Révolution Française, un nouveau calendrier est introduit (le calendrier révolutionnaire), et avec lui le système métrique de mesures de distances. La définition du mètre, proposée par Lavoisier, est « un quart de millionième de la longueur du méridien terrestre ».
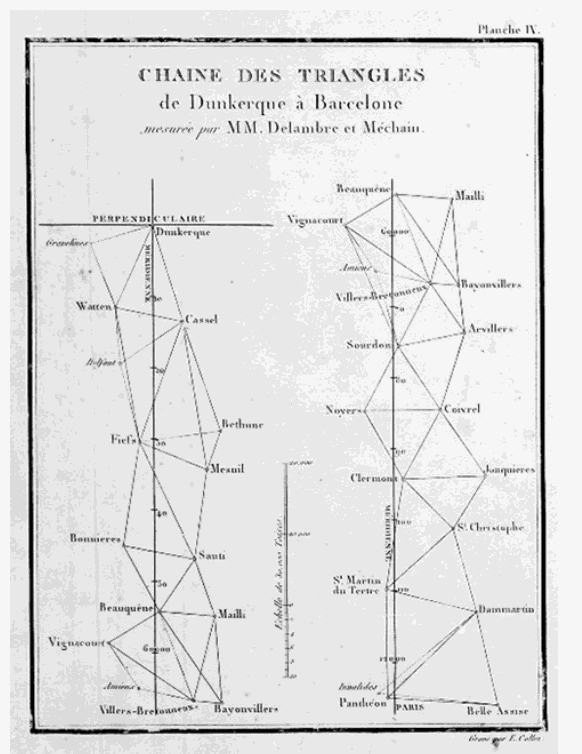
Une expédition est alors organisée pour estimer la longueur du méridien de Paris : une mesure précise de la distance entre Dunkerque et Barcelone, le long de ce méridien, est entreprise. Après plusieurs changements, ce sont finalement deux astronomes qui réalisent cette expédition, de 1792 à 1795 :Jean-Baptiste Delambre (Amiens, 1749 – Paris, 1822) (portrait de gauche ci-contre) et Pierre Méchain (Laon, 1744 – Castellon de la Plana, Espagne, 1804).
Méthode de mesure
La carte ci-contre montre les lieux des relevés effectués par Delambre et Méchain au début de leur expédition, entre Dunkerque et Paris.
En préparation de chaque mesure, un travail préparatoire était nécessaire afin de trouver des repères visuels visibles de loin (clochers, détails géographiques caractéristiques), permettant des mesures de visées précises.
D'après la figure ci-contre, quelle méthode géométrique a permis de mesurer la distance entre Dunkerque et Barcelone ?
Précision
La mesure de distance effectuée par Delambre et Méchain leur a permis de calculer la longueur du méridien terrestre, en toises, et ainsi de définir la nouvelle unité de mesure qu'le mètre.
Une étude ultérieure de leurs résultats a montré que leurs mesures de visée étaient d'une grande précision. Une erreur subsistait cependant sur le résultat final, en particulier les mesures de visées effectuées entre Perpignan et Barcelone. En effet dans cette zone l'estimation de la faussée verticale par… la masse de la chaîne des Pyrénées, qui déviait très légèrement le fil à plomb utilisé. L'effet est très faible, à la hauteur de la précision des mesures réalisées lors de cette expédition.
Pour estimer la longueur du méridien d'après la mesure effectuée, quelle méthode géométrique a été utilisée ?
Que retenir
|
La géodésie est l'étude de la forme de la Terre. La détermination de la forme de la Terre et de ses dimensions a permis, notamment, d'établir des cartes du monde spécifiques utiles notamment aux explorations et aux échanges commerciaux.
On appelle « Figure de la Terre » la représentation que nous faisons de la forme de notre planète et de ses dimensions géométriques. Cette représentation a évolué avec le temps, avec des influences propres à chaque région du monde et à chaque culture, se basant tantôt sur des arguments philosophiques tantôt sur des observations scientifiques. L'observation montre que la Terre est de forme (quasi) sphérique. Deux exemples célèbres de mesures du rayon terrestre :
|
nsidérez que raconter une belle histoire donnée du caractère. Écrire une histoire avec du caractère pour vos clients potentiels va aider à créer une relation. Cela se voit dans les petits détails comme le choix des mots ou des bizarreries comme des choix de mots ou des phrases. Écrivez avec votre point de vue, pas avec l'expérience de quelqu'un d'autre.
Les meilleures histoires sont pour tout le monde même si elles ne sont écrites que pour une seule personne. Si vous essayez d'écrire pour une audience large et générale, votre histoire sonnera fausse et fade. Personne ne sera intéressé. Écrivez-la pour une personne. Si elle est authentique pour une personne, elle le sera pour les autres.

Laisser un commentaire
Vous devez être Connecté en tant que pour poster un commentaire.