ES1ere La forme de la terre REVISER

Introduction

Application de la loi des sinus (plan de triangulation)
Conversions d'angles (degrés-radians)
Calcul de longueur d'arc de cercle (relation entre arc et angle)
Calcul de distance le long d'un parallèle ou d'un méridien

Illustration : mappemonde
Temps de travail : 20 mn

Loi des sinus - triangulation plane

Question 1

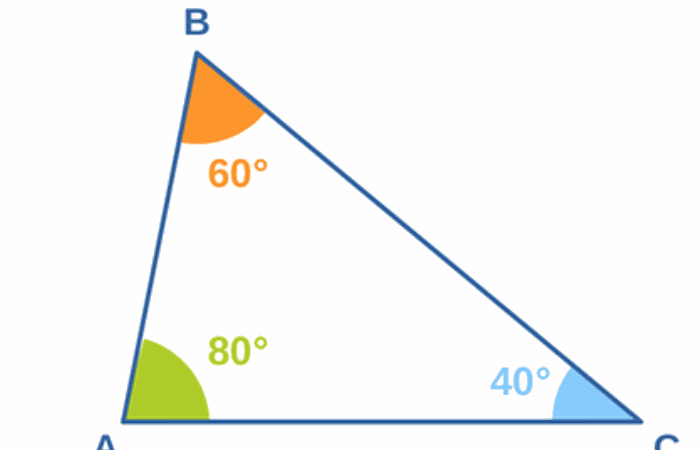
On rappelle la loi des sinus dans le triangle ABC ci-contre :

$\frac{\sin (\hat{B})}{A C} = \frac{\sin (\hat{A})}{B C} = \frac{\sin (\hat{C})}{A B}$

1. Indiquer l’expression permettant de calculer la longueur AB :

\frac{A C \times \sin (\hat{C})}{\sin (\hat{B})}

\frac{B C \times \sin (\hat{A})}{\sin (\hat{C})}

A C \times \sin (\hat{C}) \times \sin (\hat{B})

question 2

On rappelle la loi des sinus dans le triangle ABC ci-contre :

$\frac{\sin (\hat{B})}{A C} = \frac{\sin (\hat{A})}{B C} = \frac{\sin (\hat{C})}{A B}$

2. Indiquer l’expression permettant de calculer la longueur AC :

\frac{B C \times \sin (\hat{B})}{\sin (\hat{A})}

\frac{B C \times \sin (\hat{A})}{\sin (\hat{B})}

B C \times \sin (\hat{A}) \times \sin (\hat{B})

question 3

On rappelle la loi des sinus dans le triangle ABC ci-contre :

$\frac{\sin (\hat{B})}{A C} = \frac{\sin (\hat{A})}{B C} = \frac{\sin (\hat{C})}{A B}$

3. On donne AC=7km. L’angle de sommet C vaut 30° et l’angle de sommet B vaut 70°.

Calculer la longueur AB :

AB = 3,7 km

AB = 13,2 km

AB = 3,3 km

question 4

On rappelle la loi des sinus dans le triangle ABC ci-contre :

$\frac{\sin (\hat{B})}{A C} = \frac{\sin (\hat{A})}{B C} = \frac{\sin (\hat{C})}{A B}$

4. On donne BC=17km. L’angle de sommet A vaut 80° et l’angle de sommet B vaut 50°.

Calculer la longueur AC :

AC = 12,8 km

AC = 13,2 km

AC = 21,9 km

Relation entre angles et arcs

Relation entre angles et arcs

question 1

On rappelle la relation entre la longueur L d’un arc de cercle, le rayon R du cercle et l’angle au centre α (en radians) qui définit cet arc :

$L = R \times α$

Conversion degrés-radians :

Un angle de 180° vaut $π$ rad.

1. Convertir l’angle en radians : $α = 30 °$

α = π / 12 rad

α = π / 10 rad

α = π / 6 rad

question 2

On rappelle la relation entre la longueur L d’un arc de cercle, le rayon R

du cercle et l’angle au centre α (en radians) qui définit cet arc :

$L = R \times α$

Conversion degrés-radians :

Un angle de 180° vaut $π$ rad.

2. Convertir l’angle en radians : $α = 70 °$

α = 1 rad

α = 1,22 rad

α = 0,95 rad

question 3

On rappelle la relation entre la longueur L d’un arc de cercle, le rayon R du cercle

et l’angle au centre α (en radians) qui définit cet arc :

$L = R \times α$

Conversion degrés-radians :

Un angle de 180° vaut $π$ rad.

3. On donne R = 3 cm et $α = 0,5 rad$ . Calculer L :

L = 3 cm

L = 6 cm

L = 1,5 cm

question 4

On rappelle la relation entre la longueur L d’un arc de cercle, le rayon

R du cercle et l’angle au centre α (en radians) qui définit cet arc :

$L = R \times α$

Conversion degrés-radians :

Un angle de 180° vaut $π$ rad.

4. On donne R = 5 cm et $α = 30 °$ . Calculer L :

L = 5,2 cm

L = 2,6 cm

L = 2 cm

Question 5

On rappelle la relation entre la longueur L d’un arc de cercle, le rayon R du

cercle et l’angle au centre α (en radians) qui définit cet arc :

$L = R \times α$

Conversion degrés-radians :

Un angle de 180° vaut $π$ rad.

5. On donne R = 8 cm et $α = 70 °$ . Calculer L :

L = 7,6 cm

L = 9,8 cm

L = 8 cm

Distance le long d'un méridien ou d'un parallèle

question 1

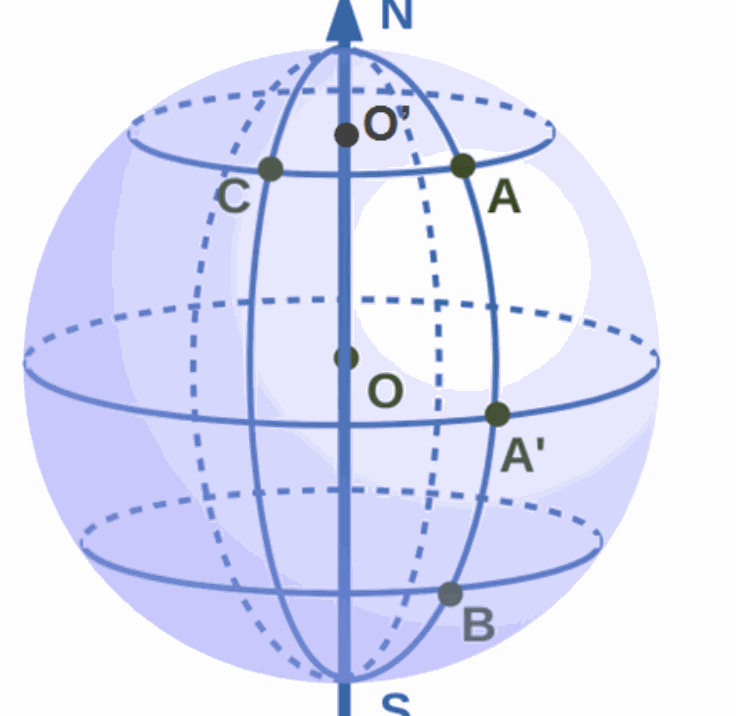
A, B et C sont trois lieux à la surface de la Terre, ayant pour coordonnées géographiques :

A (45°N, 15°E), B(30°S, 15°E), C(45°N, 35°O).

A’ est sur le méridien de A, à l’équateur.

On rappelle le rayon de la Terre : RT = 6370 km, et les relations permettant de calculer :

- la distance le long d’un méridien :

$A B = R_{T} \times | λ_{B} - λ_{A} |$

avec $λ_{A}$ et $λ_{B}$ les latitudes de A et B, en radians.

- la distance le long d'un parallèle :

$A C = R_{T} \times \cos (λ_{A}) \times | L_{C} - L_{A} |$

1. Calculer la distance entre A et A’ :

AA’ = 6370 km

AA’ = 5003 km

AA’ = 4504 km

question 3

A, B et C sont trois lieux à la surface de la Terre, ayant pour coordonnées

géographiques :

A (45°N, 15°E), B(30°S, 15°E), C(45°N, 35°O).

A’ est sur le méridien de A, à l’équateur.

On rappelle le rayon de la Terre : RT = 6370 km, et les relations permettant

de calculer :

- la distance le long d’un méridien :

$A B = R_{T} \times | λ_{B} - λ_{A} |$

avec $λ_{A}$ et $λ_{B}$ les latitudes de A et B, en radians.

- la distance le long d'un parallèle :

$A C = R_{T} \times \cos (λ_{A}) \times | L_{C} - L_{A} |$

3. Calculer la distance entre A et C :

AC = 1572km

AC = 5559 km

question 2

A, B et C sont trois lieux à la surface de la Terre, ayant pour coordonnées

géographiques :

A (45°N, 15°E), B(30°S, 15°E), C(45°N, 35°O).

A’ est sur le méridien de A, à l’équateur.

On rappelle le rayon de la Terre : RT = 6370 km, et les relations permettant

de calculer :

- la distance le long d’un méridien :

$A B = R_{T} \times | λ_{B} - λ_{A} |$

avec $λ_{A}$ et $λ_{B}$ les latitudes de A et B, en radians.

- la distance le long d'un parallèle :

$A C = R_{T} \times \cos (λ_{A}) \times | L_{C} - L_{A} |$

2. Calculer la distance entre A et B :

AB = 4504 km

AB = 8338 km

192 vues

Evaluez ce cours

ES1ere Ch1 La forme de la terre suite

Admin

Lire le suivant

ES1ere La forme de la terre REVISER

Physique chimie

Première Générale

ES1ere Ch1 La forme de la terre suite

Laisser un commentaire